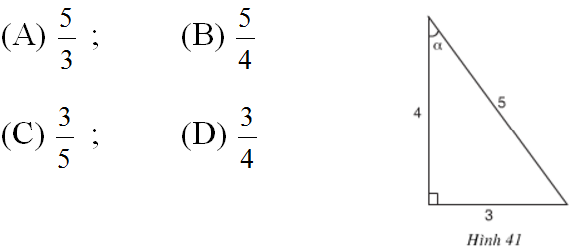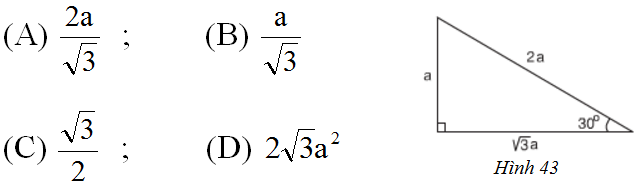Câu 42 Trang 96 - Tính
Ở một cái thang dài 3m người ta ghi: “ Để đảm bảo an toàn khi dùng thang phải đặt thang này tạo với mặt đất một góc có độ lớn từ $60^{\circ}$ đến $70^{\circ}$ ”. Đo góc thì khó hơn đo độ dài. Vậy hãy cho biết : Khi dùng thang đó chân thang phải đặt cách tường bao nhiêu mét để đảm bảo an toàn ?
-
- GDĐT Việt Nam
- Xem: 868
Câu 41 Trang 96: Tìm x, y
Tam giác ABC vuông tại C có AC = 2cm, BC = 5cm, $\widehat{BAC}=x,\widehat{ABC}=y$ . Dùng các thông tin sau ( nếu cần ) để tìm x – y :
$\sin 23^{\circ}36{}'\approx 0,4$
$\cos 66^{\circ}24{}'\approx 0,4$
$\tan 21^{\circ}48{}'\approx 0,4$
-
- GDĐT Việt Nam
- Xem: 851
Câu 40 Trang 95: Tính
Tính chiều cao của cây trong hình 50 ( làm tròn đến đề - xi – mét ) .

-
- GDĐT Việt Nam
- Xem: 843
Câu 39 Trang 95: Tính
Tìm khoảng cách giữa hai cọc để căng dây vượt qua vực trong hình 49 ( làm tròn đến mét ) .

-
- GDĐT Việt Nam
- Xem: 840
Câu 38 Trang 94: Tính
Hai chiếc thuyền A và B ở vị trí được minh họa như trong hình 48. Tính khoảng cách giữa chúng (làm tròn đến mét) .

-
- GDĐT Việt Nam
- Xem: 860
Câu 37 Trang 94: Chứng minh
Cho tam giác ABC có AB = 6cm; AC = 4,5cm; BC = 7,5cm.
a. Chứng minh tam giác ABC vuông tại A. Tính các góc B, C và đường cao AH của tam giác đó.
b. Hỏi rằng điểm M mà diện tích tam giác MBC bằng diện tích tam giác ABC nằm trên đường nào?
-
- GDĐT Việt Nam
- Xem: 957
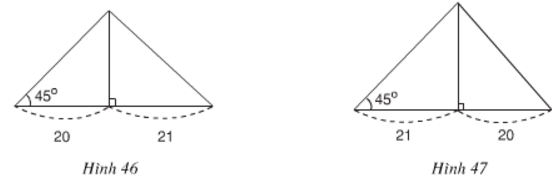
Câu 36 Trang 94 - Tính
Cho tam giác có một góc bằng $45^{\circ}$. Đường cao chia một cạnh kề với góc đó thành các phần 20cm và 21cm. Tính cạnh lớn trong hai cạnh còn lại ( lưu ý có hai trường hợp hình 46 và hình 47).
-
- GDĐT Việt Nam
- Xem: 899
Câu 35 Trang 94 - Tìm các góc
Tỉ số giữa hai cạnh góc vuông của một hình tam giác vuông bằng 19 : 28. Tìm các góc của nó.

-
- GDĐT Việt Nam
- Xem: 896
Bài 34 trang 93 - Chọn đáp án
Trong hình 44, hệ thức nào trong các hệ thức sau là đúng?

A. $\sin \alpha =\frac{b}{c}$
B. $\cot \alpha =\frac{b}{c}$
C. $\tan \alpha =\frac{a}{c}$
D. $\cot \alpha =\frac{a}{c}$
b) Trog hình 45, hệ thức nào trong các hệ thức sau không đúng ?

(A) sin2α + cos2α = 1
(B) sin α = cos β
(C) cos β = sin (90o – α)
D. $\cot \alpha =\frac{a}{c}$
-
- GDĐT Việt Nam
- Xem: 825
Bài 33 trang 93 - Tính
Chọn kết quả đúng trong các kết quả dưới đây:
a) Trong hình 41, sin α bằng:
b) Trong hình 42, sin Q bằng:
c) Trong hình 43, cos 30o bằng:
-
- GDĐT Việt Nam
- Xem: 867
Câu 32 Trang 89 - Tính
Một con thuyền với vận tốc 2km/h vượt qua một khúc sông nước chảy mạnh mất 5 phút. Biêt rằng đường đi của con thuyền tạo với bờ một góc 70∘ . Từ đó đã có thể tính được chiều rộng của khúc sông chưa ? Nếu có thể hãy tính kết quả (làm tròn đến mét) .
-
- GDĐT Việt Nam
- Xem: 856
Câu 31 Trang 89 - Tính
Trong hình 33 , AC = 8cm , AD = 9,6cm , $\widehat{ABC}=90^{\circ},\widehat{ACB}=54^{\circ},\widehat{ACD}=74^{\circ}$. Hãy tính :
a. AB .
b. $\widehat{ADC}$ .

-
- GDĐT Việt Nam
- Xem: 866
Câu 30 Trang 89
Cho tam giác ABC, trong đó BC=11cm, $\widehat{ABC}=38^{\circ},\widehat{ACB}=30^{\circ}$ . Gọi điểm N là chân của đường vuông góc kẻ từ A đến cạnh BC. Hãy tính:
a. Đoạn thẳng AN .
b. Cạnh AC.
Gợi ý: Kẻ BK vuông góc với AC.
-
- GDĐT Việt Nam
- Xem: 848
Câu 29 Trang 89
Một khúc sông sộng khoảng 250m. Một chiếc thuyền chèo qua sông bị dòng nước đẩy xiên nên phải chèo khoảng 320m mới sang được bờ bên kia. Hỏi dòng nước đã đẩy chiếc đò lệch đi một góc bằng bao nhiêu độ? (góc α trong hình 32).

-
- GDĐT Việt Nam
- Xem: 876
Câu 28 Trang 89 - Tính
Một cột đèn cao 7m có bóng trên mặt đất dài 4m. Hãy tính góc (làm tròn đến phút) mà tia sáng mặt trời tạo với mặt đất (góc α trong hình 31).

-
- GDĐT Việt Nam
- Xem: 920
Câu 27 Trang 88: Tính
>
Giải tam giác ABC vuông tại A, biết rằng :
a. $b=10cm ,\widehat{C}=30^{\circ}$
b. $c=10cm ,\widehat{C}=45^{\circ}$
c. $a=20cm ,\widehat{B}=35^{\circ}$
d. $c=21cm , b=18cm$
-
- GDĐT Việt Nam
- Xem: 840
Cây lộc vừng
Cây lộc vừng có tên khoa học là Barringtonia acutangula, là thực vật thân gỗ có đường kính lớn, hoa màu đỏ.
-
- GDĐT Việt Nam
- Xem: 1521
GDĐT Việt Nam là gì ?
Hệ thống GDĐT Việt Nam được phát triển và hướng tới lợi ích cộng đồng nhằm hỗ trợ người Việt Nam cập nhật thông tin về Giáo dục và Đạo tạo dễ dàng và hữu ích.
-
- GDĐT Việt Nam
- Xem: 2996
GDĐT là gì ?
GDĐT là viết tắt của "Giáo dục Đào tạo" trong tiếng Việt. Đây là cụm từ thường được sử dụng để chỉ toàn bộ hệ thống giáo dục và các hoạt động đào tạo trong một quốc gia.
-
- GDĐT Việt Nam
- Xem: 4814
Tiêu chí 3.6: Khu vệ sinh, hệ thống cấp thoát nước
Hướng dẫn xác định các yêu cầu (nội hàm) của các chỉ báo, gợi ý thu thập các minh chứng theo yêu cầu nội hàm của từng chỉ báo làm cơ sở để đánh giá Tiêu chí 3.6: Khu vệ sinh, hệ thống cấp thoát nước trong công tác kiểm định chất lượng giáo dục trường mầm non.
-
- GDĐT Việt Nam
- Xem: 1653