Câu 37 Trang 94: Chứng minh

Lời giải:

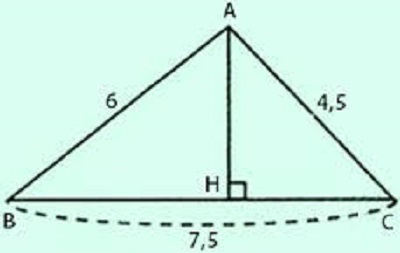
Giả sử tam giác ABC vuông tại A.

Ta phải chứng minh :  $BC^{2}=AB^{2}+AC^{2}$  

Áp dụng định lí Py-ta-go vào tam giác ABC , ta có :

$BC^{2}=AB^{2}+AC^{2}=6^{2}+(4,5)^{2}=56,25$

=>  $BC=\sqrt{56,25}=7,5$  ( cm )   ( luôn đúng )

Vậy  tam giác ABC vuông tại A .

Ta có :  $\tan B=\frac{AC}{AB}=\frac{4,5}{6}=0,75$

=>  $\widehat{B}\approx 37^{\circ}$

=>  $\widehat{C}=\widehat{A}-\widehat{B}\approx  90^{\circ}-37^{\circ}\approx 53^{\circ}$

Trong tam giác ABC vuông tại A , có AH là đường cao AH.BC=AB.AC

=> $AH=\frac{AB.AC}{BC}=\frac{4,5.6}{7,5}=3,6(cm)$

Vậy $\left\{\begin{matrix}\widehat{B}\approx 37^{\circ} &  & \\ \widehat{C}\approx 53^{\circ} &  & \\ AH=3,6(cm) &  & \end{matrix}\right.$

b.  Để $S_{\triangle MBC}=S_{\triangle ABC}$  => M cách BC một khoảng chính bằng AH .

=>  M nằm trên hai đường thẳng song song cách BC một khoảng bằng 3,6 cm .