Câu 64 Trang 92
Trên đường tròn bán kính \(R\) lần lượt đặt theo cùng một chiều, kể từ điểm \(A\), ba cung \(\overparen{AB}\), \(\overparen{BC}\), \(\overparen{CD}\) sao cho: \(sđ\overparen{AB}\)=\(60^0\), \(sđ\overparen{BC}\)=\(90^0\), \(sđ\overparen{CD}\)=\(120^0\)
a) Tứ giác \(ABCD\) là hình gì?
b) Chứng minh hai đường chéo của tứ giác \(ABCD\) vuông góc với nhau.
c) Tính độ dài các cạnh của tứ giác \(ABCD\) theo \(R\).
-
- GDĐT Việt Nam
- Xem: 823
Câu 63 Trang 92
Vẽ các hình lục giác đều, hình vuông, hình tam giác đều cùng nội tiếp đường tròn (O;R) rồi tính cạnh của các hình đó theo R.
-
- GDĐT Việt Nam
- Xem: 1256
Câu 62 Trang 91
a) Vẽ tam giác ABC cạnh a=3cm.
b) Vẽ đường tròn (O;R) ngoại tiếp tam giác đều ABC. Tính R.
c) Vẽ đường tròn (O;r) nội tiếp tam giác đều ABC. Tính r.
d) Vẽ tiếp tam giác đều IJK ngoại tiếp đường tròn (O;R).
-
- GDĐT Việt Nam
- Xem: 1017
Câu 61 Trang 91
a) Vẽ đường tròn tâm O, bán kính 2cm.
b) Vẽ hình vuông nội tiếp đường tròn (O) ở câu a)
c) Tính bán kính r của đường tròn nội tiếp hình vuông ở câu b) rồi vẽ đường tròn (O;r).
-
- GDĐT Việt Nam
- Xem: 905
Câu 60 Trang 90
Xem hình 48. Chứng minh QR // ST.
Hướng dẫn: Xét cặp góc so le trong $\widehat{PST},\widehat{SRQ}$

-
- GDĐT Việt Nam
- Xem: 818
Câu 59 Trang 90
Cho hình bình hành ABCD. Đường tròn đi qua ba đỉnh A, B, C cắt đường thẳng CD tại P khác C. Chứng minh AP = AD.
-
- GDĐT Việt Nam
- Xem: 851
Câu 58 Trang 89
Cho tam giác đều ABC. Trên nửa mặt phẳng bờ BC không chứa đỉnh A, lấy điểm D sao cho
DB = DC, $\widehat{DCB}=\frac{1}{2}.\widehat{ACB}$
a) Chứng minh ABCD là tứ giác nội tiếp.
b) Xác định tâm của đường tròn đi qua bốn điểm A, B, C, D.
-
- GDĐT Việt Nam
- Xem: 848
Câu 57 Trang 89
Trong các hình sau, hình nào nội tiếp được trong một đường tròn:
Hình bình hành, hình chữ nhật, hình vuông, hình thang, hình thang vuông, hình thang cân? Vì sao?
-
- GDĐT Việt Nam
- Xem: 890
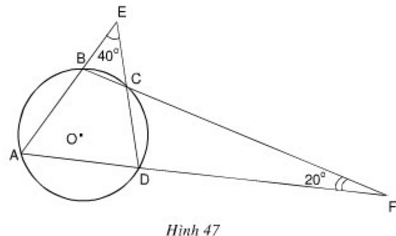
Bài 56 trang 89
Xem hình 47. Hãy tìm số đo các góc của tứ giác ABCD.
-
- GDĐT Việt Nam
- Xem: 911
Câu 55 Trang 89
Cho ABCD là một tứ giác nội tiếp đường tròn tâm M, biết $\widehat{DAB}=80^{\circ}$, $\widehat{DAM}=30^{\circ}$, $\widehat{BMC}=70^{\circ}$. Hãy tính số đo các góc $\widehat{MAB}$, $\widehat{BCM}$, $\widehat{AMB}$, $\widehat{DMC}$, $\widehat{AMD}$, $\widehat{MCD}$ và $\widehat{BCD}$.
-
- GDĐT Việt Nam
- Xem: 1056
Câu 54 Trang 89
Tứ giác ABCD có $\widehat{ABC}+\widehat{ADC}=180^{\circ}$.
Chứng minh rằng các đường trung trực của AC, BD, AB cùng đi qua một điểm
-
- GDĐT Việt Nam
- Xem: 821
Bài 53 trang 89
Biết ABCD là tứ giác nội tiếp. Hãy điền vào ô trống trong bẳng sau (nếu có thể).
-
- GDĐT Việt Nam
- Xem: 1265
Bài 52 trang 87
"Góc sút" của quả phạt đền 11 mét là bao nhiêu độ? Biết rằng chiều rộng cầu môn là 7,32m. Hãy chỉ ra hai vị trí khác trên sân có cùng "góc sút" như quả phạt đền 11 mét.
-
- GDĐT Việt Nam
- Xem: 1206
Câu 51 Trang 87
Cho I, O lần lượt là tâm đường tròn nội tiếp, tâm đường tròn ngoại tiếp tam giác ABC với A = $60^{\circ}$. Gọi H là giao điểm của các đường cao BB'và CC'.
Chứng minh các điểm B, C, O, H, I cùng thuộc một đường tròn.
-
- GDĐT Việt Nam
- Xem: 818
Câu 50 Trang 87
Cho đường tròn đường kính AB cố định, M là một điểm chạy trên đường tròn. Trên tia đối của tia MA lấy điểm I sao cho MI = 2MB.
a) Chứng minh $\widehat{AIB}$ không đổi.
b) Tìm tập hợp các điểm I nói trên
-
- GDĐT Việt Nam
- Xem: 819