Câu 51 Trang 87

Lời giải

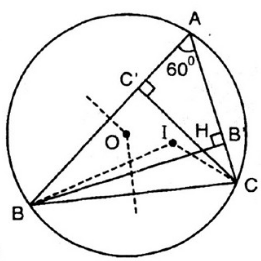
Ta có: $\widehat{BOC}$ là góc ở tâm chắn cung BC và $\widehat{BAC}$ là góc nội tiếp chắn cung BC

=> $\widehat{BAC}$  = $\frac{1}{2}$ $\widehat{BOC}$ (định lý về góc nội tiếp và góc ở tâm)

=> $\widehat{BOC}$ = $2$ . $\widehat{BAC}$ = $2.60^{\circ}$     (1)

Xét tứ giác AC'HB" có" $\widehat{A}+\widehat{HC'A}+\widehat{HB'A}+\widehat{B'HC'}=360^{\circ}$ (tổng 4 góc trong tứ giác)

=> $\widehat{B'HC'}$ = $360^{\circ}-60^{\circ}-90^{\circ}-90^{\circ}=120^{\circ}$

mà $\widehat{B'HC'}$ đối đỉnh $\widehat{BHC}$ => $\widehat{BHC}$ = $120^{\circ}$    (2)

Trong $\Delta IBC$:

BI là tia phân giác $\widehat{ABC}$ =>  $\widehat{CBI}$ = $\frac{1}{2}$ $\widehat{ABC}$

CI là tia phân giác $\widehat{ACB}$ =>  $\widehat{BCI}$ = $\frac{1}{2}$ $\widehat{ACB}$

=> $\widehat{CBI}$  + $\widehat{BCI}$ = $\frac{1}{2}$ ($\widehat{ABC}$ + $\widehat{ACB}$)

               = $\frac{1}{2}$ . $\left(180^{\circ}-\widehat{BAC}\right)$ = $\frac{1}{2}$ . $\left (180^{\circ}-60^{\circ}\right)$

               = $60^{\circ}$

=> $\widehat{BIC}$ = $180^{\circ}-\widehat{CBI}$ = $180^{\circ}-60^{\circ}$ = $120^{\circ}$   (3)

Từ (1)(2)(3), các điểm O, I, H nằm trên cung chứa góc $120^{\circ}$ dựng trên đoạn BC 

Vậy 5 điểm B, C, O, H, I nằm trên cùng 1 đường tròn