Câu 58 Trang 89

Lời giải 

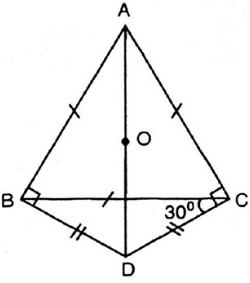
a) Tam giác ABC đều => $\widehat{ACB}$ = $60^{\circ}$

Mà: $\widehat{DCB}=\frac{1}{2}.\widehat{ACB}$ (gt) => $\widehat{DCB}=30^{\circ}$

=> $\widehat{ACD}=\widehat{DCB}+\widehat{ACB}=60^{\circ}+30^{\circ}=90^{\circ}$

Xét $\Delta ABD$ và $\Delta ACD$ có:

AD chung

BD = CD (gt)

AB = AC (do tam giác ABC đều)

=> $\Delta ABD=\Delta ACD$ (c.c.c)

=> $\widehat{ABD}=\widehat{ACD}$  (2 góc tương ứng)

=> $\widehat{ABD}=\widehat{ACD}=90^{\circ}$

=> $\widehat{ABD}+\widehat{ACD}=180^{\circ}$

=> Tứ giác ABCD nội tiếp.

b) Ta có tam giác ACD vuông tại C (do $\widehat{ACD}=90^{\circ}$), gọi O là trung điểm của AD

=> OC là đường trung tuyến ứng với cạnh huyền AD của tam giác ACD.

=> OC = OA = OD

=> A, C, D cùng thuộc đường tròn tâm O.

Tương tự, OB là trung tuyến ứng với cạnh huyền AD của tam giác ABD

=> OA = OB = OD

=> A, B, D cùng thuộc đường tròn (O)

 => 4 điểm A, B, C, D cùng nằm trên đường tròn tâm O.