Câu 64 Trang 92

Lời giải

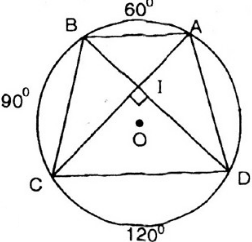
a) \(\widehat {BA{\rm{D}}} = {{{{90}^0} + {{120}^0}} \over 2} = {105^0}\) (góc nội tiếp chắn \(\overparen{BCD}\))     (1)

\(\widehat {A{\rm{D}}C} = {{{{60}^0} + {{90}^0}} \over 2} = {75^0}\) ( góc nội tiếp chắn\(\overparen{ABC}\) )          (2)

Từ (1) và (2) có:

\(\widehat {BA{\rm{D}}} + \widehat {A{\rm{D}}C} = {105^0} + {75^0} = {180^0}\) (3)

Mà \(\widehat {BA{\rm{D}}}\) và \(\widehat {A{\rm{D}}C}\) là hai góc trong cùng phía tạo bởi cát tuyến \(AD\) và hai đường thẳng \(AB, CD\).

=> \(AB // CD\). Do đó tứ giác \(ABCD\) là hình thang.

Mà $ABCD$ nội tiếp hình tròn nên $ABCD$ là hình thang cân.

Vậy \(ABCD\) là hình thang cân.

(\(BC = AD\) và \(sđ\overparen{BC}\)=\(sđ\overparen{AD}\)=\(90^0\))

b) Gọi $I$ là giao của hai đường chéo \(AC\) và \(BD\).

\(\widehat {CI{\rm{D}}}\) là góc có đỉnh nằm trong đường tròn, chắn cung CD và cung AB, nên:

\(\widehat{CI{\rm{D}}}\)=\(\frac{sđ\overparen{AB}+sđ\overparen{CD}}{2}\)=\({{{{60}^0} +{{120}^0}} \over 2} = {90^0}\)

Vậy \(AC \bot BD\)

c)

Vì \(sđ\overparen{AB}\) = \(60^0\) nên \(\widehat {AOB} = {60^0}\) (góc ở tâm)

Lại có: $\Delta AOB$ cân tại $O$ (vì $OA=OB=R$)

\(=> ∆AOB\) đều => \(AB = R\)

Ta có: $\Delta COD$ cân tại $O$ (vì $OC=OD=R$)

lại có: \(sđ\overparen{BC}\)= \(90^0\) => \(\widehat {COD} = {90^0}\) => $\Delta COD$ vuông cân tại O

=> $BC=\sqrt{2.OB^2}=R.\sqrt{2}$

Vì $ABCD$ là hình thang cân nên $AD=BC=R.\sqrt2$

Ta có: \(sđ\overparen{CD}\)= \(120^0\) => \(\widehat {COD} = {120^0}\)

Từ $O$ kẻ $OH\perp CD,H\in CD$ => \(\widehat {COH} = \frac{1}{2}.\widehat{COD}={60^0}\)

Trong $\Delta COH$ vuông tại $H$ có:

$tan COH=\frac{CH}{OC}=>tan {60^0}=\frac{CH}{R}=>CH=R.\sqrt{3}$

Vậy các cạnh của tứ giác $ABCD$ có độ dài: $BC=AD=R.\sqrt{2};AB=R;CD=R.\sqrt{3}$