Câu 55 Trang 89

Lời giải

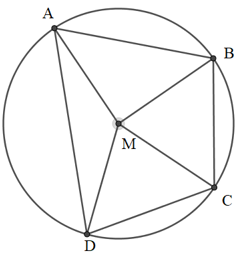
Ta có: $\widehat{MAB}=\widehat{DAB}-\widehat{DAM}={80}^o-{30}^o={50}^o$ (1)

Xét tam giác MBC có:

MB = MC (cùng bằng bán kính đường tròn (O))

Do đó, tam giác MBC cân tại M

$\Rightarrow \widehat{BCM}=\widehat{CBM}=\frac{{180}^o-\widehat{BMC}}{2}=\frac{{180}^o-{70}^o}{2}={55}^o$

Xét tam giác MAB có:

MA = MB (cùng bằng bán kính đường tròn (O))

Do đó, tam giác MAB cân tại M

$\Rightarrow \widehat{MAB}=\widehat{MBA}$

$\Rightarrow \widehat{AMB}={180}^o-2\widehat{MAB}={180}^o-{2.50}^o={80}^o$

Ta có: Góc BAD là góc nội tiếp chắn cung BCD

$\Rightarrow \widehat{BAD}=\frac{1}{2}$sđ$\stackrel{⏜}{BCD}$

$\Rightarrow$sđ $\stackrel{⏜}{BCD}=2\widehat{BAD}={2.80}^o={160}^o$

Mà ta có:

Góc BMC là góc ở tâm chắn cung nhỏ BC $\Rightarrow$sđ$\stackrel{⏜}{BC}=\widehat{BMC}={70}^o$

sđ $\stackrel{⏜}{DC}=$sđ$\stackrel{⏜}{BCD}-$ sđ $\stackrel{⏜}{BC}={160}^o-{70}^o={90}^o$

Mà góc DMC là góc ở tâm chắn cung nhỏ DC $\Rightarrow \widehat{DMC}={90}^o$

Xét tam giác MAD có:

MA = MD (cùng bằng bán kính đường tròn (O))

Do đó, tam giác MAD cân tại M

$\Rightarrow \widehat{MAD}=\widehat{MDA}$

$\Rightarrow \widehat{AMD}={180}^o-2.\widehat{MAD}={180}^o-{2.30}^o={120}^o$

Xét tam giác MCD có:

MC = MD (cùng bằng bán kính đường tròn (O))

$\widehat{DMC}={90}^o$ (chứng minh trên)

Do đó, tam giác MCD vuông cân tại M

$\Rightarrow \widehat{MDC}=\widehat{MCD}={45}^o$

Ta lại có: Tia CM là tia nằm giữa hai tia CB, CD nên ta có:

$\widehat{BCD}=\widehat{BCM}+\widehat{MCD}={55}^o+{45}^o={100}^o$.