Câu 16 Trang 106: So sánh
Cho đường tròn (O), điểm A nằm bên trong đường tròn. Vẽ dây BC vuông góc với OA tại A. Vẽ dây EF bất kì đi qua A và không vuông góc với OA. Hãy so sánh độ dài hai dây BC và EF.
-
- GDĐT Việt Nam
- Xem: 849
Câu 15 Trang 106: So sánh
Cho hình 70 trong đó hai đường tròn cùng có tâm là O. Cho biết AB > CD .

Hãy so sánh các độ dài :
a. OH và OK .
b. ME và MF .
c. MH và MK .
-
- GDĐT Việt Nam
- Xem: 828
Câu 14 Trang 106: Tính
Cho đường tròn tâm O bán kính 25cm, dây AB bằng 40cm. Vẽ dây CD song song với AB và có khoảng cách đến AB bằng 22cm. Tính độ dài dây CD.
-
- GDĐT Việt Nam
- Xem: 852
Câu 13 Trang 106: Chứng minh
Cho đường tròn (O) có các dây AB và CD bằng nhau, các tia AB và CD cắt nhau tại điểm E nằm bên ngoài đường tròn. Gọi H và K theo thứ tự là trung điểm của AB và CD. Chứng minh rằng:
a. EH = EK.
b. EA = EC.
-
- GDĐT Việt Nam
- Xem: 1034
Câu 12 Trang 106: Tính
Cho đường tròn tâm O bán kính 5cm, dây AB bằng 8 cm.
a) Tính khoảng cách từ tâm O đến dây AB.
b) Gọi I là điểm thuộc dây AB sao cho AI=1cm. Kẻ dây CD đi qua I và vuông góc với AB. Chứng minh rằng CD=AB.
-
- GDĐT Việt Nam
- Xem: 898
Câu 11 Trang 104: Chứng minh
Cho đường tròn (O) đường kính AB, dây CD không cắt đường kính AB. Gọi H và K theo thứ tự là chân các đường vuông góc kẻ từ A và B đến CD.
Chứng minh rằng CH = DK.
Gợi ý: Kẻ OM vuông góc với CD.
-
- GDĐT Việt Nam
- Xem: 891
Câu 10 Trang 104: Chứng minh
Cho tam giác ABC, các đường cao BD và CE. Chứng minh rằng:
a) Bốn điểm B, E, D, C cùng thuộc một đường tròn.
b) DE
-
- GDĐT Việt Nam
- Xem: 903
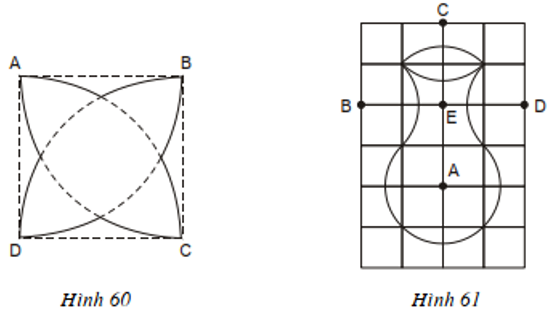
Bài 9 trang 101 - Đố
Đố
a) Vẽ hình hoa bốn cánh. Hình hoa bốn cánh trên hình 60 được tạo bởi các cung có tâm A, B, C, D (trong đó A, B, C, D là các đỉnh của một hình vuông và tâm của cung là tâm của đường tròn chứa cung đó). Hãy vẽ lại hình 60 vào vở.
b) Vẽ lọ hoa. Chiếc lọ hoa trên hình 61 được vẽ trên giấy kẻ ô vuông bởi năm cung có tâm A, B, C, D, E. Hãy vẽ lại hình 61 vào giấy kẻ ô vuông.
-
- GDĐT Việt Nam
- Xem: 1027
Câu 8 Trang 101: Dựng góc
Cho góc nhọn xAy và hai điểm B, C thuộc Ax. Dựng đường tròn (O) đi qua B và C sao cho tâm O nằm trên tia Ay.
-
- GDĐT Việt Nam
- Xem: 839
Câu 7 Trang 101: Nối
Hãy nối mỗi ô ở cột trái với một ô ở cột phải để được khẳng định đúng :

-
- GDĐT Việt Nam
- Xem: 888
Câu 6 Trang 100: Đố
Trong các biển báo giao thông sau, biển nào có tâm đối xứng, biển nào có trục đối xứng ?
a. Biển cấm đi ngược chiều (h.58) .
b. Biển cấm ôtô ( h.59 ).

-
- GDĐT Việt Nam
- Xem: 836
Câu 5 Trang 100: Giải đố
Đố. Một tấm bìa hình tròn không còn dấu vết của tâm. Hãy tìm lại tâm của hình tròn đó.
-
- GDĐT Việt Nam
- Xem: 843
Câu 4 Trang 100: Xác định vị trí
Trên mặt phẳng tọa độ Oxy, hãy xác định vị trí của mỗi điểm A( -1 ; -1 ) , B( -1 ; -2 ) ,C(2–√,2–√) đối với đường tròn tâm O bán kính 2
-
- GDĐT Việt Nam
- Xem: 887
Câu 3 Trang 100: Chứng minh
Chứng minh các định lý sau :
a. Tâm của đường tròn ngoại tiếp tam giác vuông là trung điểm của cạnh huyền.
b. Nếu một tam giác có một cạnh là đường kính của đường tròn ngoại tiếp thì tam giác đó là tam giác vuông.
-
- GDĐT Việt Nam
- Xem: 860
Câu 2 Trang 100
Hãy nối mỗi ô ở cột trái với mỗi ô ở cột phải để được khẳng định đúng.

-
- GDĐT Việt Nam
- Xem: 856