Câu 63 Trang 92

Lời giải

a)

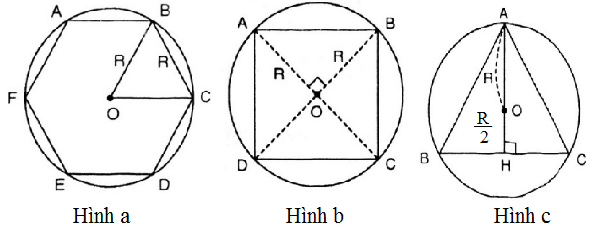
* Vẽ lục giác đều nội tiếp (O; R) :

+ Lấy điểm A trên (O ; R).

+ Vẽ cung tròn (A; R) cắt (O; R) tại B và F⇒AB = AF = R

+ Vẽ cung tròn (B; R) cắt (O; R) tại C (khác A)⇒ BC = R

+ Vẽ cung tròn (C; R) cắt (O; R) tại D (khác B)⇒ CD = R

+ Vẽ cung tròn (D; R) cắt (O; R) tại E (khác C)⇒ DE = R

ABCDEF là lục giác đều cần vẽ.

* Tính cạnh: AB = BC = CD = DE = EF = FA = R.

b)

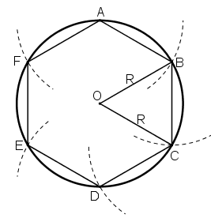
* Vẽ hình vuông:

+ Vẽ đường kính AC của đường tròn tâm O.

+ Vẽ đường kính BD ⊥ AC

Tứ giác ABCD có hai đường chéo bằng nhau, vuông góc với nhau và cắt nhau tại trung điểm mỗi đường nên là hình vuông.

Nối A với B ; B với C ; C với D với A ta được hình vuông ABCD nội tiếp đường tròn (O).

* Tính cạnh :

ΔAOB vuông tại O

$\Rightarrow AB=\sqrt{O{A}^2+O{B}^2}=\sqrt{R^2+R^2}=R\sqrt{2}$

c)

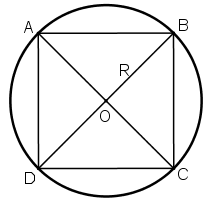
* Vẽ tam giác đều:

Chia đường tròn thành 6 cung bằng nhau như phần a).

Nối các điểm như hình vẽ ta được tam giác đều nội tiếp đường tròn.

* Tính cạnh tam giác:

Gọi cạnh ΔABC đều là a.

Gọi H là trung điểm BC

⇒ HB = $\frac{a}{2}$

$\Rightarrow AH=\sqrt{A{B}^2-H{B}^2}=\sqrt{a^2-{\left(\frac{a}{2}\right)}^2}=\frac{a\sqrt{3}}{2}$

Tam giác ABC là tam giác đều có O là tâm đường tròn ngoại tiếp đồng thời là trọng tâm tam giác.

$\Rightarrow OA=\frac{2}{3}AH=\frac{2}{3}.\frac{a\sqrt{3}}{2}=\frac{a\sqrt{3}}{3}=\frac{a}{\sqrt{3}}$

Mà OA = R ⇒ a = R$\sqrt{3}$.

Vậy tam giác đều có cạnh là R$\sqrt{3}$.