Câu 54 Trang 89

Lời giải

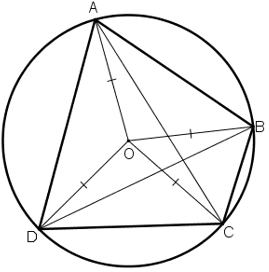
Tứ giác ABCD có $\widehat{ABC}+\widehat{ADC}=180^{\circ}$

nên ABCD là tứ giác nội tiếp đường tròn.

Gọi tâm đường tròn đó là O, ta có: $OA = OB = OC = OD = R$

$OA = OB$ nên ΔOAB cân tại O, đường trung tuyến kẻ từ O cũng chính là đường cao của tam giác.

⇒ O thuộc đường trung trực của AB

$OB = OD$ nên ΔOBD cân tại O, đường trung tuyến kẻ từ O cũng chính là đường cao của tam giác.

⇒ O thuộc đường trung trực của BD

$OA = OC$ nên ΔOAC cân tại O, đường trung tuyến kẻ từ O cũng chính là đường cao của tam giác.

⇒ O thuộc đường trung trực của AC.

⇒ O thuộc đường trung trực của AC, BD, AB .

Vậy các đường trung trực của AC, BD, AB cùng đi qua O.

 => các đường trung trực của AB, BD, AC cùng đi qua 1 điểm là . (đpcm)