Câu 19 Trang 75
Cho đường tròn tâm O, đường kính AB và S là một điểm nằm bên ngoài đường tròn. SA và SB lần lượt cắt đường tròn tại M, N. Gọi H là giao điểm của BM và AN. Chứng minh rằng SH vuông góc với AB.
-
- GDĐT Việt Nam
- Xem: 882
Câu 18 Trang 75
Một huấn luyện viên cho cầu thủ tập sút bóng vào cầu môn PQ. Bóng được đặt ở các vị trí A, B, C trên một cung trong như hình 20. Hãy so sánh các góc $\widehat{PAQ}$, $\widehat{PBQ}$, $\widehat{PCQ}$.

-
- GDĐT Việt Nam
- Xem: 989
Câu 17 Trang 75
Muốn xác định tâm của một đường tròn mà chỉ dùng êke thì phải làm như thế nào?
-
- GDĐT Việt Nam
- Xem: 849
Câu 16 Trang 75
Xem hình 19 (hai đường tròn có tâm là B, C và điểm B nằm trên đường tròn tâm C).
a) Biết $\widehat{MAN}$ = $30^{\circ}$, tính $\widehat{PCQ}$
b) Nếu $ \widehat{PCQ}$ = $136^{\circ}$ thì $ \widehat{MAN}$ có số đo là bao nhiêu?

-
- GDĐT Việt Nam
- Xem: 959
Câu 15 Trang 75
Các khẳng định sau đây đúng hay sai?
a) Trong một đường tròn, các góc nội tiếp cùng chắn một cung thì bằng nhau.
b) Trong một đường tròn, các góc nội tiếp bằng nhau thì cùng chắn một cung.
-
- GDĐT Việt Nam
- Xem: 954
Câu 14 Trang 72
a) Chứng minh rằng đường kính đi qua điểm chính giữa của một cung thì đi qua trung điểm của dây căng cung ấy. Mệnh đề đảo có đúng không? Hãy nêu thêm điều kiện để mệnh đề đảo đúng.
b) Chứng minh rằng đường kính đi qua điểm chính giữa của một cung thì vuông góc với dây căng cung ấy và ngược lại
-
- GDĐT Việt Nam
- Xem: 908
Câu 13 Trang 72
Chứng minh rằng trong một đường tròn, hai cung bị chắn giữa hai dây song song thì bằng nhau.
-
- GDĐT Việt Nam
- Xem: 907
Câu 12 Trang 72
Cho tam giác ABC. Trên tia đối của tia AB lấy một điểm D sao cho AD = AC. Vẽ đường tròn tâm O ngoại tiếp tam giác DBC.
Từ O lần lượt hạ các đường vuông góc OH, OK với BC và BD ( H ∈ BC, K ∈ BD )
a) Chứng minh rằng OH > OK.
b) So sánh hai cung nhỏ BD và BC.
-
- GDĐT Việt Nam
- Xem: 849
Câu 11 Trang 72
Cho hai đường tròn bằng nhau (O) và (O') cắt nhau tại hai điểm A và B. Kẻ các đường kính AOC, AO'D. Gọi E là giao điểm thứ hai của AC với đường tròn (O') .
a) So sánh các cung nhỏ BC, BD.
b) Chứng mình rằng B là điểm chính giữa của cung EBD (tức là điểm B chia cung EBD thành hai cung bằng nhau: cung BE = cung BD)
-
- GDĐT Việt Nam
- Xem: 898
Câu 10 Trang 71
a) Vẽ đường tròn tâm O, bán kính R = 2cm. Nêu cách vẽ cung AB có số đo bằng 60∘. Hỏi dây AB dài bao nhiêu xentimet?
b) Làm thế nào để chia được đường tròn thành sáu cung bằng nhau như trên hình 12?

Hình 12
-
- GDĐT Việt Nam
- Xem: 852
Câu 9 Trang 70
Trên đường tròn tâm O lấy ba điểm A, B, C sao cho góc AOB = 100∘, số đo cung AC = 45∘. Tính số đo của cung nhỏ BC và cung lớn BC. (Xét cả hai trường hợp: điểm C nằm trên cung nhỏ AB, điểm C nằm trên cung lớn AB).
-
- GDĐT Việt Nam
- Xem: 850
Bài 8 trang 70
Mỗi khẳng định sau đây đúng hay sai? Vì sao?
a) Hai cung bằng nhau thì số đo bằng nhau.
b) Hai cung có số đo bằng nhau thì bằng nhau.
c) Trong hai cung, cung nào có số đo lớn hơn là cung lớn.
d) Trong hai cung trên một đường tròn, cung nào có số đo nhỏ hơn thì nhỏ hơn.
-
- GDĐT Việt Nam
- Xem: 859
Bài 7 trang 69
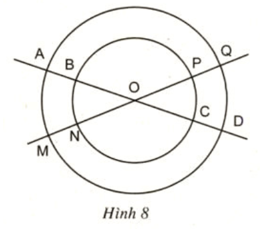
Cho hai đường tròn cùng tâm O với bán kính khác nhau. Hai đường thẳng đi qua O cắt hai đường tròn đó tại các điểm A, B, C, D, M, N, P, Q (h.8).
a) Em có nhận xét gì về số đo của các cung nhỏ AM, CP, BN, DQ?
b) Hãy nêu tên các cung nhỏ bằng nhau.
c) Hãy nêu tên hai cung lớn bằng nhau.
-
- GDĐT Việt Nam
- Xem: 752
Bài 5 trang 69
Hai tiếp tuyến của đường tròn (O) tại A và B cắt nhau tại M. Biết góc AMB = 35o.
a) Tính số đo của góc ở tâm tạo bởi bán kính OA, OB.
b) Tính số đo mỗi cung AB (cung lớn và cung nhỏ).
-
- GDĐT Việt Nam
- Xem: 832
Bài 4 trang 69
Xem hình 7. Tính số đo của góc ở tâm AOB và số đo cung lớn AB.
-
- GDĐT Việt Nam
- Xem: 852