Câu 12 Trang 106: Tính

Lời giải:

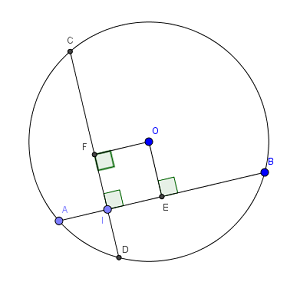
a.  Kẻ  $OE\perp AB=>EA=EB=4(cm)$

Xét tam giác OEB vuông tại H , có:  $OE^{2}=OB^{2}-EB^{2}=5^{2}-4^{2}=9$

=>  OE = 3 (cm ).

Vậy khoảng cách từ tâm O đến dây AB chính bằng OE = 3cm .

b.    Kẻ  $OF\perp CD$ .

Xét tứ giác FOEI có ba góc vuông

=> FOEI  là hình chữ nhật .

=>  OF = EI. 

Ta có : EA = 4 (cm) , AI = 1 (cm)

=> EI  = 4 - 1 = 3 (cm)  => OF = 3 (cm)

=>  OE = OF = 3 (cm).

=>  Hai dây AB và CD cách đều tâm nên chúng bằng nhau  <=> AB=CD.  ( đpcm )