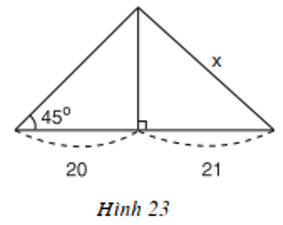
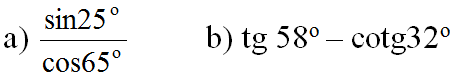Câu 28 Trang 89 - Tính
Một cột đèn cao 7m có bóng trên mặt đất dài 4m. Hãy tính góc (làm tròn đến phút) mà tia sáng mặt trời tạo với mặt đất (góc α trong hình 31).

-
- GDĐT Việt Nam
- Xem: 938
Câu 27 Trang 88: Tính
>
Giải tam giác ABC vuông tại A, biết rằng :
a. $b=10cm ,\widehat{C}=30^{\circ}$
b. $c=10cm ,\widehat{C}=45^{\circ}$
c. $a=20cm ,\widehat{B}=35^{\circ}$
d. $c=21cm , b=18cm$
-
- GDĐT Việt Nam
- Xem: 864
Câu 26 Trang 88 - Tính
Các tia nắng mặt trời tạo với mặt đất một góc xáp xỉ bằng 34∘ và bóng của một tháp trên mặt đất dài 86m (H.30). Tính chiều cao của tháp (làm tròn đến mét).

-
- GDĐT Việt Nam
- Xem: 856
Bài 25 trang 84 - So sánh
So sánh:
a) tan25o và sin 25o ; b) cot 32o và cos32o
c) tan45o và cos45o ; d) cot60o và sin30o
-
- GDĐT Việt Nam
- Xem: 859
Bài 24 trang 84 - Sắp xếp
Sắp xếp các tỉ số lượng giác sau theo thứ tự tăng dần:
a) sin78o, cos14o, sin 47o, cos87o
b) tan73o, cot25o, tan62o, cot38o
-
- GDĐT Việt Nam
- Xem: 840
Bài 22 trang 84 - So sánh
So sánh:
a) sin 20o và sin 70o ; b) cos25o và cos63o15'
c) tan 73o20' và 45o ; d) cot 2o và cot 37o40'
-
- GDĐT Việt Nam
- Xem: 917
Bài 21 trang 84 - Tìm x
Dùng bảng lượng giác hoặc máy tính bỏ túi để tìm góc nhọn x (làm tròn kết quả đến độ), biết rằng:
a) sin x = 0,3495;
b) cos x = 0,5427;
c) tan x = 1,5142;
d) cot x = 3,163.
-
- GDĐT Việt Nam
- Xem: 996
Bài 20 trang 84 - Tính
Dùng bảng lượng giác (có sử dụng phần hiệu chính) hoặc máy tính bỏ túi, hãy tìm các tỉ số lượng giác sau (làm tròn đến chữ số thập phân thứ tư):
a) sin70o13' ;
b) cos25o32';
c) tan43o10' ;
d) cot32o15'
-
- GDĐT Việt Nam
- Xem: 843
Bài 19 trang 84 - Tính
Dùng bảng lượng giác hoặc máy tính bỏ túi để tìm số đo của góc nhọn x (làm tròn đến phút), biết rằng:
a) sin x = 0,2368;
b) cos x = 0,6224;
c) tan x = 2,154;
d) cot x = 3,251.
-
- GDĐT Việt Nam
- Xem: 876
Bài 18 trang 83 - Tính
Dùng bảng lượng giác hoặc máy tính bỏ túi để tìm các tỉ số lượng giác sau (làm tròn đến chữ số thập phân thứ tư):
a) sin40o12' ;
b) cos52o54';
c) tan63o36' ;
d) cot25o18'
-
- GDĐT Việt Nam
- Xem: 880
Bài 16 trang 77 - Tính
Cho tam giác vuông có một góc 60o và cạnh huyền có độ dài là 8. Hãy tìm độ dài của cạnh đối diện với góc 60o.
-
- GDĐT Việt Nam
- Xem: 943
Bài 15 trang 77 - Tỉ số lượng giác
Cho tam giác ABC vuông tại A. Biết cos B = 0,8. Hãy tính các tỉ số lượng giác của góc C.
Gợi ý: Sử dụng bài tập 14.
-
- GDĐT Việt Nam
- Xem: 881
Bài 14 trang 77 - Chứng minh
Sử dụng định nghĩa các tỉ số lượng giác của một góc nhọn để chứng minh rằng: Với góc nhọn α tùy ý, ta có:
a) , tanα.cotα = 1;
b) sin2α + cos2α = 1.
Gợi ý: Sử dụng định lí Py-ta-go.
-
- GDĐT Việt Nam
- Xem: 826