Bài 14 trang 77 - Chứng minh

Lời giải:

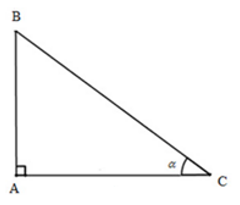
a) Xét tam giác ABC vuông tại A có $\widehat{A}={90}^o$

=> $\widehat{B}+\widehat{C}={90}^o$

=> $\widehat{C}<{90}^o$

Đặt $\widehat{C}=\alpha$

Hay α < 90°

Do đó α là góc nhọn.

Các tỉ số lượng giác của góc $\widehat{C}=\alpha$ là:

sinα = sin C = $\frac{AB}{BC}$

cosα = cosC = $\frac{AC}{BC}$

tanα = tanC = $\frac{AB}{AC}$

cotα = cotC = $\frac{AC}{AB}$

Ta thấy rằng:

$\frac{\sin \alpha }{cos\alpha }=\frac{\frac{AB}{BC}}{\frac{AC}{BC}}=\frac{AB}{AC}$ => tanα = $\frac{\sin \alpha }{cos\alpha }\left(=\frac{AB}{AC}\right)$ (đcpcm)

$\frac{cos\alpha }{\sin \alpha }=\frac{\frac{AC}{BC}}{\frac{AB}{BC}}=\frac{AC}{AB}$ => cotα = $\frac{cos\alpha }{\sin \alpha }\left(=\frac{AC}{AB}\right)$ (đcpcm)

tanα.cotα = $\frac{AB}{AC}.\frac{AC}{AB}$ = 1 (đcpcm)

b)

Xét tam giác ABC vuông tại A

Áp dụng định lí Py-ta-go ta có:

BC² = AB² + AC² (1)

Mặt khác ta có:

sin²α = ${\left(\frac{AB}{BC}\right)}^2=\frac{A{B}^2}{B{C}^2}$

cos²α = ${\left(\frac{AC}{BC}\right)}^2=\frac{A{C}^2}{B{C}^2}$

=> sin²α + cos²α = $\frac{A{B}^2}{B{C}^2}+\frac{A{C}^2}{B{C}^2}=\frac{A{B}^2+A{C}^2}{B{C}^2}$ (2)

Từ (1) và (2) ta có: sin²α + cos²α = $\frac{B{C}^2}{B{C}^2}$ = 1 (đcpcm).