Lời giải

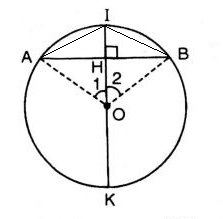
a) Vì I là điểm chính giữa của cung AB, suy ra cung IA = cung IB => IA = IB (liên hệ giữa cung và dây)

Ta có: OA = OB = bán kính. Suy ra đường kính IK là đường trung trực của dây AB. 

Vậy HA = HB (đpcm)

Mệnh đề đảo: Đường kính đi qua trung điểm của một dây thì đi qua điểm chính giữa của cung căng dây đó.

Chứng minh: Vì ΔAOB cân tại O và HA = HB nên OH là đường phân giác của $\widehat{AOB}$. 

Suy ra $\widehat{O_{1}}$ = $\widehat{O_{2}}$

Từ đó suy ra cung IA = cung IB

Tuy nhiên điều này không thể xảy ra khi dây AB đi qua tâm O của đường tròn.

Vậy phải thêm điều kiện để mệnh đề đảo đúng là: Đường kính đi qua trung điểm của một dây không đi qua tâm thì đi qua điểm chính giữa của cung căng dây đó.

b) Ta có: I là điểm chính giữa cung AB => cung IA = cung IB => IA = IB => I nằm trên trung trực của AB.  (1)

Lại có: OA = OB (= bán kính) => O nằm trên trung trực của AB                                                                   (2)

Từ (1), (2) suy ra: OI là trung trực của AB => OI $\perp $ AB (đpcm)

Ngược lại: Ta có dây cung AB, bán kính OI $\perp$ AB, cần chứng minh I là điểm chính giữa cung AB

Xét tam giác OAB cân tại O (OA = OB) có OH là đường cao

=> OH đồng thời là đường phân giác

=> $\widehat{O_{1}}$ = $\widehat{O_{2}}$

=> cung IA = cung IB (định lý về góc ở tâm)

=> Điểm I là điểm chính giữa cung AB (đpcm)