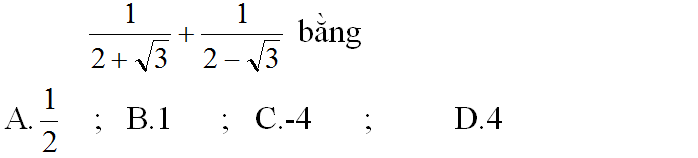Câu 75 Trang 40: Chứng minh đẳng thức

Chứng minh các đẳng thức sau :

a.  $\left ( \frac{2\sqrt{3}-\sqrt{6}}{\sqrt{8}-2}-\frac{\sqrt{216}}{3} \right ).\frac{1}{\sqrt{6}}=-1,5$

b.  $\left ( \frac{\sqrt{14}-\sqrt{7}}{1-\sqrt{2}}+\frac{\sqrt{15}-\sqrt{5}}{1-\sqrt{3}} \right ):\frac{1}{\sqrt{7}-\sqrt{5}}=-2$

c.  $\frac{a\sqrt{b}+b\sqrt{a}}{\sqrt{ab}}:\frac{1}{\sqrt{a}-\sqrt{b}}=a-b$  ( với a , b >0 và $a\neq b$ )

d.  $\left ( 1+\frac{a+\sqrt{a}}{\sqrt{a}+1} \right )\left ( 1-\frac{a-\sqrt{a}}{\sqrt{a}-1} \right )=1-a$  ( với $a\geq 0,a\neq 1$ )

Câu 74 Trang 40: Tìm x

Tìm x , biết :

a.  $\sqrt{(2x-1)^{2}}=3$

b.  $\frac{5}{3}\sqrt{15x}-\sqrt{15x}-2=\frac{1}{3}\sqrt{15x}$

Câu 73 Trang 40: Rút gọn biểu thức

Rút gọn rồi tính giá trị của các biểu thức sau :

a.  $\sqrt{-9a}-\sqrt{9+12a+4a^{2}}$  tại a = - 9

b.  $1+\frac{3m}{m-2}\sqrt{m^{2}-4m+4}$  tại m = 1,5

c.  $\sqrt{1-10a+25a^{2}}-4a$  tại $a=\sqrt{2}$

d.  $4x-\sqrt{9x^{2}+6x+1}$  tại $x=-\sqrt{3}$

Câu 72 Trang 40: Phân tích thành nhân tử

Phân tích thành nhân tử  ( với các số x, y, a, b không âm và a ≥ b )

a.  $xy-y\sqrt{x}+\sqrt{x}-1$

b.  $\sqrt{ax}-\sqrt{by}+\sqrt{bx}-\sqrt{ay}$

c.  $\sqrt{a+b}+\sqrt{a^{2}-b^{2}}$

d.  $12-\sqrt{x}-x$

Câu 71 Trang 40: Rút gọn biểu thức

Rút gọn các biểu thức sau :

a.  $(\sqrt{8}-3\sqrt{2}+\sqrt{10})\sqrt{2}-\sqrt{5}$

b.  $0,2.\sqrt{(-10^{2}).3}+2\sqrt{(\sqrt{3}-\sqrt{5})^{2}}$

c.  $\left ( \frac{1}{2}\sqrt{\frac{1}{2}}-\frac{3}{2} \sqrt{2}+\frac{4}{5}\sqrt{200}\right ):\frac{1}{8}$

d.  $2\sqrt{(\sqrt{2}-3)^{2}}+\sqrt{2(-3)^{2}}-5\sqrt{(-1)^{4}}$

Câu 70 Trang 40: Biến đổi, rút gọn biểu thức

>Câu 70: Trang 40 - sgk toán 9 tập 1

Tìm giá trị các biểu thức sau bằng cách biến đổi, rút gọn thích hợp :

a. $\sqrt{\frac{25}{81}.\frac{16}{49}.\frac{196}{9}}$

b. $\sqrt{3\frac{1}{16}.2\frac{14}{25}.2\frac{34}{81}}$

c. $\frac{\sqrt{640}.\sqrt{34,3}}{\sqrt{567}}$

d. $\sqrt{21,6}.\sqrt{810}.\sqrt{11^{2}-5^{2}}$

Câu 69 Trang 36: So sánh

So sánh :

a.  5 và $\sqrt[3]{123}$

b.  $5\sqrt[3]{6}$ và $6\sqrt[3]{5}$

Câu 68 Trang 36: Tính

Tính :

a. $\sqrt[3]{27}-\sqrt[3]{-8}-\sqrt[3]{125}$

b. $\frac{\sqrt[3]{135}}{\sqrt[3]{5}}-\sqrt[3]{54}.\sqrt[3]{4}$

Bài 67 trang 36 - Tính

Hãy tính 3√512; 3√−729; 3√0,064; 3√−0,216; 3√−0,008

Bài 66 trang 34 - Chọn câu trả lời đúng

Giá trị của biểu thức

Hãy chọn câu trả lời đúng.