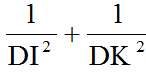Bài 16 trang 77 - Tính

Cho tam giác vuông có một góc 60^o và cạnh huyền có độ dài là 8. Hãy tìm độ dài của cạnh đối diện với góc 60^o.

• 
• David Smith
• February 10, 2022

Bài 15 trang 77 - Tỉ số lượng giác

Cho tam giác ABC vuông tại A. Biết cos B = 0,8. Hãy tính các tỉ số lượng giác của góc C.

Gợi ý: Sử dụng bài tập 14.

• 
• David Smith
• February 10, 2022

Bài 14 trang 77 - Chứng minh

Sử dụng định nghĩa các tỉ số lượng giác của một góc nhọn để chứng minh rằng: Với góc nhọn α tùy ý, ta có:

a) $\tan \alpha =\frac{\sin \alpha }{cos\alpha },\cot \alpha =\frac{cos\alpha }{\sin \alpha }$, tanα.cotα = 1;

b) sin²α + cos²α = 1.

Gợi ý: Sử dụng định lí Py-ta-go.

• 
• David Smith
• February 10, 2022

Bài 13 trang 77 - Dựng góc

Dựng góc nhọn α, biết:

a) sinα = $\frac{2}{3}$;

b) cosα = 0,6;

c) tanα = $\frac{3}{4}$;

d) cotα = $\frac{3}{2}$.

• 
• David Smith
• February 10, 2022

Bài 12 trang 76 - Tỉ số lượng giác

Hãy viết các tỉ số lượng giác sau thành tỉ số lượng giác của các góc nhỏ hơn 45^o: sin60^o, cos75^o, sin52^o30', cot82^o, tan80^o

• 
• David Smith
• February 10, 2022

Bài 11 trang 76 - Tỉ số lượng giác

 Cho tam giác ABC vuông tại C, trong đó AC = 0,9m, BC = 1,2m. Tính các tỉ số lượng giác của góc B, từ đó suy ra các tỉ số lượng giác của góc A.

• 
• David Smith
• February 10, 2022

Bài 10 trang 76 - Tỉ số lượng giác

Vẽ một tam giác vuông có một góc nhọn 34^o rồi viết các tỉ số lượng giác của góc 34^o.

• 
• David Smith
• February 10, 2022

Bài 9 trang 70 - Chứng minh

Cho hình vuông ABCD. Gọi I là một điểm nằm giữa A và B. Tia DI và tia CB cắt nhau ở K. Kẻ đường thẳng qua D, vuông góc với DI. Đường thẳng này cắt đường thẳng BC tại L. Chứng minh rằng:

a) Tam giác DIL là một tam giác cân

b) Tổng

không đổi khi I thay đổi trên cạnh AB.

• 
• David Smith
• February 10, 2022

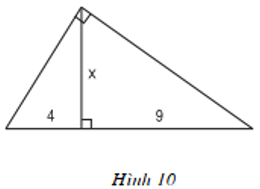
Bài 8 trang 70 - Tính

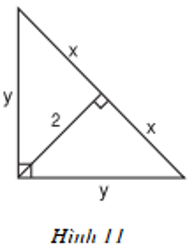
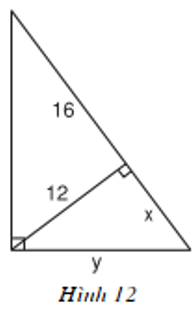
Tìm x và y trong mỗi hình sau:

a) 

b) 

c) 

• 
• David Smith
• February 10, 2022

Bài 7 trang 69 - Chứng minh

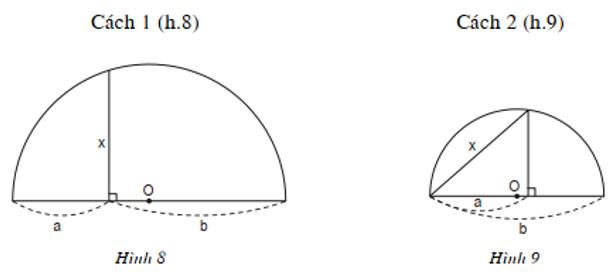
 Người ta đưa ra cách vẽ đoạn trung bình nhân x của hai đoạn thẳng a, b (tức là x² = ab) như trong hai hình sau:

Dựa vào các hệ thức (1) và (2) hãy chứng minh các cách vẽ trên là đúng.

Gợi ý: Nếu một tam giác có đường trung tuyến ứng với một cạnh bằng nửa cạnh đó thì tam giác ấy là tam giác vuông.

• 
• David Smith
• February 10, 2022