Quản lý thông tin trường học PM Ăn bán trú
Hướng dẫn quản lý thông tin trường học trong PM Ăn bán trú
-
- GDĐT Việt Nam
- Xem: 198
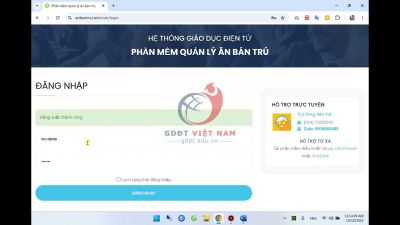
Đăng nhập PM Ăn bán trú
Hướng dẫn đăng nhập phần mềm quản lý ăn bán trú
-
- GDĐT Việt Nam
- Xem: 333
Những di sản thế giới của Việt Nam được UNESCO công nhận
🇻🇳 NHỮNG DI SẢN THẾ GIỚI CỦA VIỆT NAM (Theo danh sách được UNESCO công nhận)
-
- GDĐT Việt Nam
- Xem: 153 - APP
Bạch tuộc – Nhà ảo thuật tài ba dưới đáy biển
🐙 Bạch tuộc – Nhà ảo thuật tài ba dưới đáy biển
-
- GDĐT Việt Nam
- Xem: 163 - APP
Voi – Người khổng lồ có trí nhớ tuyệt vời
🐘 Voi – Người khổng lồ có trí nhớ tuyệt vời
-
- GDĐT Việt Nam
- Xem: 196 - APP
Abraham Lincoln (1809 – 1865) – vị tổng thống vĩ đại của nước Mỹ
🤝 Abraham Lincoln – Người gieo hạt giống tự do và bình đẳng
-
- GDĐT Việt Nam
- Xem: 300 - APP
Thomas Edison (1847 – 1931)
💡 Thomas Edison – Nhà phát minh làm sáng cả thế giới
-
- GDĐT Việt Nam
- Xem: 278 - APP
Thời Trần – Tinh thần hiếu học và quân sự
🏰 Bài học lịch sử: Thời Trần – Tinh thần hiếu học và quân sự “Hội nghị Diên Hồng – Cả nước một lòng chống giặc ngoại xâm”
-
- GDĐT Việt Nam
- Xem: 187 - APP
Đặc sản biển đảo Việt Nam
🐠 BÀI HỌC DÀNH CHO TRẺ: KHÁM PHÁ ĐẶC SẢN BIỂN ĐẢO VIỆT NAM 🦀🌊
-
- GDĐT Việt Nam
- Xem: 316 - APP
Vòng tuần hoàn của nước
💧 Vòng tuần hoàn của nước – Mưa từ đâu mà có?
-
- GDĐT Việt Nam
- Xem: 194 - APP