Bài 26 trang 115 - Tính chất của hai tiếp tuyến cắt nhau

Lời giải:

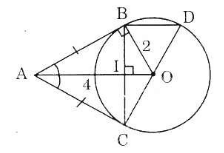
a) Ta có: AB = AC (tính chất của hai tiếp tuyến cắt nhau). Nên ΔABC cân tại A.

Lại có AO là tia phân giác của góc A nên AO ⊥ BC. (trong tam giác cân, đường phân giác cũng là đường cao)

b) Gọi I là giao điểm của AO và BC. Suy ra BI = IC (đường kính vuông góc với một dây).

Xét ΔCBD có :

CI = IB

CO = OD (bán kính)

⇒ BD//OI (OI là đường trung bình của tam giác BCD).

Vậy BD//AO.

c) Ta có: OC = OB = 2 cm (bán kính)

Theo định lí Pi-ta-go trong tam giác vuông OAC (tính chất tiếp tuyến):

AC² = OA² – OC² = 4² – 2² = 12

=> AC = $\sqrt{12}=2\sqrt{3}$ (cm)

Lại có: $\sin \widehat{OAC}=\frac{OC}{OA}=\frac{2}{4}=\frac{1}{2}\Rightarrow \widehat{OAC}=30°$

Suy ra: $\widehat{BAC}=2\widehat{OAC}$ = 2.30° = 60°.

Tam giác ABC cân tại A có $\widehat{BAC}=60°$ nên ABC là tam giác đều.

Do đó AB = BC = AC = $2\sqrt{3}$ (cm).