Bài 30 trang 116 - Tính chất của hai tiếp tuyến cắt nhau

Lời giải:

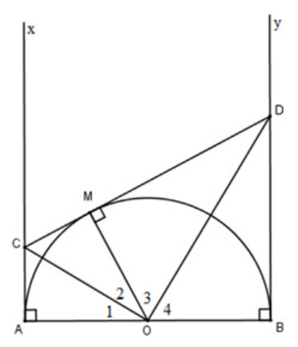
Theo đề bài, ta có:

OA ⊥ Ax tại A, OB ⊥ By tại B

Do đó, Ax, By là các tiếp tuyến của nửa đường tròn lần lượt tại A và B

Vì CA, CM là hai tiếp tuyến của (O) lần lượt tại A và M, theo tính chất hai tiếp tuyến cắt nhau, ta có: CM = CA và $\widehat{O_1}=\widehat{O_2}$

Vì DB, DM là hai tiếp tuyến của đường tròn (O) lần lượt tại B và M, theo tính chất hai tiếp tuyến cắt nhau, ta có: DM = DB và $\widehat{O_3}=\widehat{O_4}$

a)

Ta có:

$\widehat{O_1}+\widehat{O_2}+\widehat{O_3}+\widehat{O_4}={180}^o$

⇔ $\widehat{O_2}+\widehat{O_2}+\widehat{O_3}+\widehat{O_3}={180}^o$ (do $\widehat{O_1}=\widehat{O_2}$, $\widehat{O_3}=\widehat{O_4}$)

⇔ $2\widehat{O_2}+2\widehat{O_3}={180}^o$

⇔ $\widehat{O_2}+\widehat{O_3}={90}^o$

⇔ $\widehat{COD}={90}^o$.

b)

Ta có: CM = AC, MD = BD (chứng minh trên)

Lại có: CD = CM + MD = AC + BD (đpcm)

c)

Ta có: CM = AC, MD = BD (chứng minh trên)

Xét tam giác COD vuông tại O có OM là đường cao (tính chất tiếp tuyến).

Áp dụng hệ thức lượng trong tam giác vuông có:

R² = MO² = MC . MD = AC . BD (do MO = R)

Vì bán kính đường tròn không đổi khi M di chuyển trên nửa đường tròn nên MO² không đổi do đó tích AC. BD không đổi khi M di chuyển trên nửa đường tròn.