Bài 32 trang 116 - Tính chất của hai tiếp tuyến cắt nhau

Lời giải:

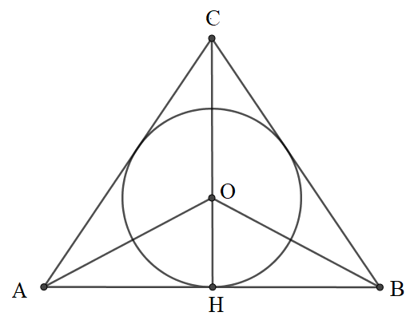
Gọi (O) là đường tròn nội tiếp tam giác đều ABC và H là tiếp điểm thuộc AB

Khi đó OH = 1cm là bán kính của (O)

Do đó, O là giao điểm của ba đường trung trực của tam giác ABC (do tam giác ABC đều)

=> CH ⊥ AB

Xét tam giác đều ABC

CH ⊥ AB

Do đó CH là đường cao và cũng là đường trung tuyến ứng với cạnh BC (tính chất của tam giác đều)

Mặt khác, O cũng là trọng tâm của tam giác ABC (tính chất của tam giác đều)

Theo tính chất đường trung tuyến ta có:

OH = $\frac{1}{3}$CH => CH = 3OH = 3.1 = 3 (cm)

Ta lại có: $\widehat{ABC}={60}^o$ (do ABC là tam giác đều) hay $\widehat{HBC}={60}^o$

Xét tam giác CHB vuông tại H

Có:

$\widehat{HBC}={60}^o$

CH = 3cm

Áp dụng hệ thức giữa cạnh và góc trong tam giác vuông ta có:

CH = CB.$\sin \widehat{HBC}$ => CB = $\frac{CH}{\sin \widehat{HBC}}=\frac{3}{\sin {60}^o}=2\sqrt{3}$

=> AB = AC = BC = $2\sqrt{3}$ (cm)

Do đó, diện tích tam giác ABC là: S = $\frac{1}{2}$CH.AB = $\frac{1}{2}$.3.$2\sqrt{3}$ = $3\sqrt{3}$ (cm²)

Ta chọn đáp án (D).