Câu 46 Trang 86

Lời giải

Dựng hình

- Dựng đoạn thẳng $AB=3cm$ (dùng thước đo chia khoảng mm)

- Dựng góc $\widehat{BAx}$ = $55^{\circ}$ (dùng thước đo góc và thước thẳng)

- Dựng tia $Ay$ vuông góc với $Ax$ (dùng êke)

- Dựng đường trung trực $d$của đoạn thẳng $AB$ (dùng thước có chia khoảng và êke). Gọi O là giao điểm của d và Ay.

- Dựng đường tròn tâm $O$, bán kính $OA$ (dùng compa)

Ta có: cung AmB là cung chứa góc $55^{\circ}$ dựng trên đoạn $AB=3cm$

Chứng minh

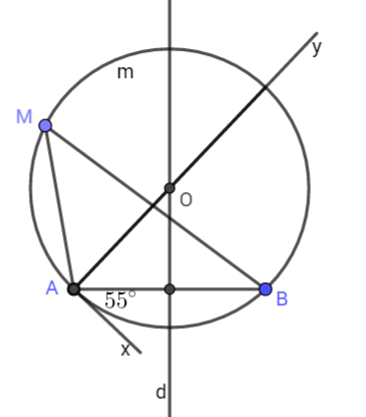
Ta có: AB là dây cung đường tròn (O), Ax là tiếp tuyến với (O) tại A => $\widehat{BAx}$ là góc tạo bởi tia tiếp tuyến và dây cung AB

=> số đo cung AB = $\widehat{BAx}$ = $55^{\circ}$

Lấy M bất kỳ thuộc cung AmB => $\widehat{AMB}$ là góc nội tiếp chắn cung AB => $\widehat{AMB}$ = số đo cung AB = $55^{\circ}$

=> số đo cung AmB = $55^{\circ}$

Vậy AmB là cung chắn góc $55^{\circ}$ dựng trên đoạn AB = 3cm.