Câu 44 Trang 86

Lời giải

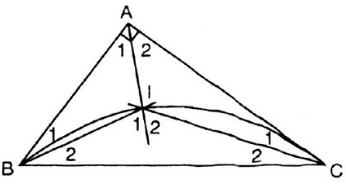
BI là tia phân giác $\widehat{ABC}$ =>  $\widehat{B_{1}}$ = $\widehat{B_{2}}$ = $\frac{1}{2}$ $\widehat{ABC}$

CI là tia phân giác $\widehat{ACB}$ =>  $\widehat{C_{1}}$ = $\widehat{C_{2}}$ = $\frac{1}{2}$ $\widehat{ACB}$

=> $\widehat{B_{1}}$  + $\widehat{C_{1}}$ = $\widehat{B_{2}}$ + $\widehat{C_{2}}$ = $\frac{1}{2}$ ($\widehat{ABC}$ + $\widehat{ACB}$)

               = $\frac{1}{2}$ . $90^{\circ}$ (Do tam giác ABC vuông tại A nên $\widehat{ABC}$ + $\widehat{ACB}$ = $90^{\circ}$)

               = $45^{\circ}$

Ta có: $\widehat{I_{1}}$ = $\widehat{A_{1}}$ + $\widehat{B_{1}}$ (tính chất góc ngoài $\Delta ABI$)

           $\widehat{I_{2}}$ = $\widehat{A_{2}}$ + $\widehat{C_{1}}$ (tính chất góc ngoài $\Delta ACI$)

=> $\widehat{I_{1}}$ + $\widehat{I_{2}}$ = $\widehat{A_{1}}$ + $\widehat{B_{1}}$ + $\widehat{A_{2}}$ + $\widehat{C_{1}}$ 

=> $\widehat{BIC}$ = $\widehat{A_{1}}$ + $\widehat{A_{2}}$  + $\widehat{B_{1}}$  + $\widehat{C_{1}}$

               = $90^{\circ}$ + $45^{\circ}$ = $135^{\circ}$

=> Điểm I luôn nhìn đoạn thẳng BC dưới 1 góc không đổi là $135^{\circ}$, vậy quỹ tích điểm I là cung chứa góc $135^{\circ}$ dựng trên đoạn thẳng BC.