Bài 4: Một số hệ thức về cạnh và góc trong tam giác vuông
-
- GDĐT Việt Nam
- 14/06/2023 - Xem: 1373


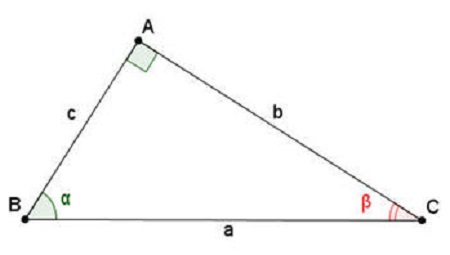
Định lí
=> Ta có các hệ thức sau :
Trong một tam giác vuông , nếu biết hai cạnh hoặc một cạnh và một góc nhọn ta sẽ tìm được tất cả các cạnh và góc còn lại của nó .
=> Đó là bài toán " Giải tam giác vuông " .
Ví dụ minh họa :
Cho tam giác LMN vuông tại L có $\widehat{M}=51^{\circ}$ , LM = 2,8 .Hãy giải tam giác vuông LNM .
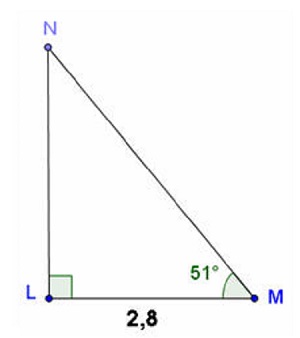
Hướng dẫn giải :
Ta có : $\widehat{N}=90^{\circ}-\widehat{M}=90^{\circ}-51^{\circ}=39^{\circ}$
Theo hệ thức giữa cạnh và góc trong tam giác vuông LMN , ta có :
$LN=LM.\tan M=2,8.\tan 51^{\circ}$\approx 3,458
$MN=\frac{LM}{\cos 51^{\circ}}\approx \frac{2,8}{0,6293}\approx 4,449$
Vậy tam giác LNM có : $\left\{\begin{matrix}LM=2,8 & & \\ LN \approx 3,458& & \\ MN\approx 4,449 & & \end{matrix}\right.$ và $\left\{\begin{matrix}\widehat{L}= 90^{\circ}& & \\ \widehat{N}= 39^{\circ} & & \\ \widehat{M}= 51^{\circ} & & \end{matrix}\right.$
Lưu ý :
Đăng ký tài khoản ngay bây giờ để sử dụng các tiện ích chuyển đổi số của GDĐT Việt Nam.