Câu 39 Trang 83

Lời giải

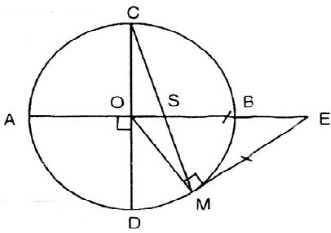
 AB, CD là 2 đường kính vuông góc => ta có 4 góc ở tâm là các góc vuông.

=> $\widehat{AOD}$ = $\widehat{AOC}$ = $\widehat{BOD}$ =$\widehat{BOC}$ = $90^{\circ}$

=> sđ cung AD = sđ cung AC = sđ cung BD = sđ cung BC = $90^{\circ}$

Ta có: $\widehat{EMS}$ là góc tạo bởi tia tiếp tuyến ME và dây cung MC => $\widehat{EMS}$ = $\frac{1}{2}$ . sđ cung MC (1) 

Lại có: $\widehat{BSM}$ là góc có đỉnh nằm trong đường tròn (O) => $\widehat{BSM}$ = $\frac{1}{2}$ . (sđ cung AC + sđ cung BM)

Vì sđ cung AC = sđ cung BC (cmt) => $\widehat{BSM}$ = $\frac{1}{2}$ . (sđ cung BC + sđ cung BM) = $\frac{1}{2}$ . sđ cung MC   (2)

Từ (1) (2) => $\widehat{EMS}$ = $\widehat{BSM}$  (= $\frac{1}{2}$ . sđ cung MC)

=> $\Delta ESM$ là tam giác cân tại E (dấu hiệu nhận biết tam giác cân)

=> $ES = EM$