Câu 35 Trang 80

Lời giải

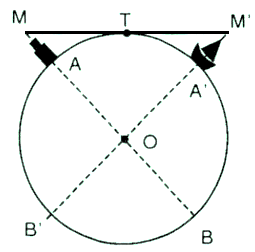
Đỉnh ngọn hải đăng là điểm M, vị trí mà người quan sát trên tàu là điểm M’.

O là tâm trái đất, M’A’ là khoảng cách từ người quan sát trên tàu tới mặt nước biển => $M’A = 10 (m) = 0,01 (km)$

MA là độ cao của ngọn hải đăng => $MA = 40 (m) = 0,04 (km)$

MT là tiếp tuyến của đường tròn (O), MA là cát tuyến của (O), theo kết quả bài 34, ta có: $MT^{2}=MA.MB$ 

Mặt khác: $MB = MA + 2 . AB = MA + 2.R$

Thay số vào đẳng thức trên ta có: $MT^{2}=0,04.(0,04+2.6400)=512,0016$

=> $MT\approx23$ (km)

Tương tự, M’T là tiếp tuyến của (O) => $M’T^{2}=M’A’.M’B’$  = $0,01.(0,01+2.6400)=128,0001$

=> $M’T\approx11$ (km)

 Từ đó: $MM’=MT+M’T\approx23+11\approx34$ (km)