Câu 23 Trang 76

Lời giải

Trường hợp điểm M nằm bên trong hình tròn

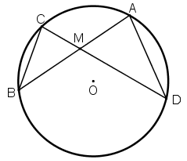
Xét hai tam giác $MAB’$ và $MA’B$ có:

$\widehat{M_{1}}$ = $\widehat{M_{2}}$ (đối đỉnh)

$\widehat{AB’M}$ = $\widehat{ABM}$ (hai góc nội tiếp cùng chắn cung AA’)

=> $\Delta MAB’\sim \Delta MA’B$                                                                                                    

=> $\frac{MA}{MA’}=\frac{MB’}{MB}$

=> $MA.MB=MB’.MA’$ (đpcm)

 

Trường hợp điểm M nằm bên ngoài hình tròn 

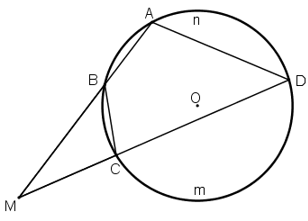
$\Delta MAB’\sim \Delta MA’B$ vì:

$\widehat{AB’M}$ = $\widehat{ABM}$ (hai góc nội tiếp cùng chắn cung AA’)

$\widehat{M}$ chung

=> $\frac{MA}{MA’}=\frac{MB’}{MB}$

 => $MA.MB=MB’.MA’$ (đpcm)