Câu 22 Trang 76

Lời giải

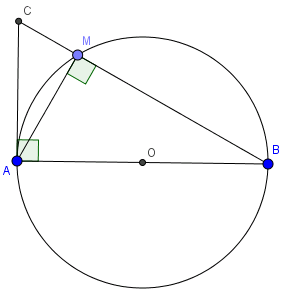
Ta có: $ \widehat{AMB}$ là góc nội tiếp chắn nửa đường tròn => $\widehat{AMB}$ = $90^{\circ}$.

CA là tiếp tuyến của (O) tại A (gt) => $\widehat{CAB}$ = $90^{\circ}$

Xét hai tam giác MAB và MCA có:

$\widehat{MAB}$ = $\widehat{MCA}$ (cùng phụ với $ \widehat{MAC}$)

$\widehat{MBA}$ = $\widehat{MAC}$ (cùng phụ với $ \widehat{MAB}$)

=> $\Delta MAB\sim \Delta MCA$

=> $\frac{MA}{MB}=\frac{MC}{MA}$

 => $MA^{2}=MB.MC$ (đpcm)