Câu 25 Trang 112

Lời giải:

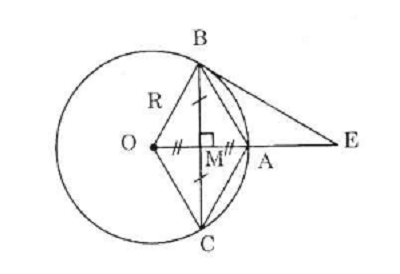
a.  Ta có :  $OA\perp BC$  => MB = MC .

Mà :  MO = MA  ( gt )

=>  Tứ giác OBAC là hình bình hành  ( vì có các đường chéo cắt nhau tại trung điểm mỗi đường )

=> OBAC là hình thoi .  ( vì có hai đường chéo vuông góc ).

=> BA = BO = OA

=> Tam giác AOB là tam giác đều .

=>  $\widehat{BOA}=60^{\circ}$

b.  Vì EB là tiếp tuyến  => $EB\perp OB$

Xét $\triangle BOE$ vuông tại B, ta có : $BE=BO.\tan 60^{\circ}=R\sqrt{3}$

Vậy  $BE=R\sqrt{3}$ .