Câu 24 Trang 111: Chứng minh

Lời giải:

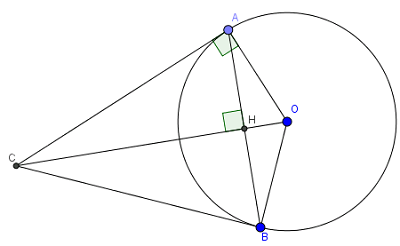
a.  Gọi H là giao điểm của OC và AB.

Ta có :

• $\triangle OAB$ cân tại O (OA = OB, bán kính)
• OH là đường cao nên cũng là đường phân giác.

=>  $\widehat{AOC}=\widehat{BOC}$

Xét $\triangle OBC$ và $\triangle OAC$ , ta có : 

• OB = OC  ( bán kính )
• $\widehat{AOC}=\widehat{BOC}$
• OC cạnh chung

=> $\triangle OBC$ = $\triangle OAC$  ( c-g-c )

=>  $\widehat{OBC}=\widehat{OAC}=90^{\circ}$

Vậy CB là tiếp tuyến của đường tròn (O). (đpcm)

b.  Ta có : $AH=\frac{AB}{2}=\frac{24}{2}=12(cm)$

Xét $\triangle OAH$ vuông tại H , ta có :  $OA^{2}=OH^{2}+AH^{2}$

=> $OH^{2}=OA^{2}-AH^{2}=15^{2}-12^{2}=81$

=> $OH=\sqrt{81}=9(cm)$

Xét $\triangle OAB$ vuông tại A , ta có : $OA^{2}=OH.OC$

=> $OC=\frac{OA^{2}}{OH}=\frac{15^{2}}{9}=25(cm)$

Vậy độ dài OC = 25cm .