Lời giải:

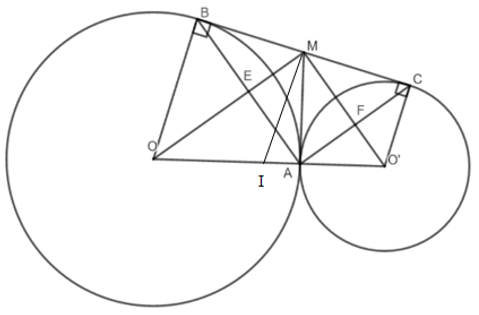
a)

Ta có: MB, MA là tiếp tuyến của đường tròn (O) nên MA = MB (tính chất hai tiếp tuyến cắt nhau) (1)

Ta lại có MA, MC là tiếp tuyến của đường tròn (O’) nên MA = MC (tính chất hai tiếp tuyến cắt nhau) (2)

Từ (1) và (2) suy ra MA = MB = MC => MA = $\frac{1}{2}$BC

Xét tam giác ABC

Có MA là trung tuyến và MA = $\frac{1}{2}$BC

Do đó, tam giác ABC vuông tại A

=> $\widehat{BAC}={90}^o$

Xét tam giác MBA cân tại M (do MA = MB )

Có EM là phân giác (tính chất hai tiếp tuyến cắt nhau) nên ME cũng là đường cao

=> ME ⊥ AB => $\widehat{AEM}={90}^o$

Xét tam giác MCA cân tại M (do MA = MC)

Có FM là phân giác (tính chất hai tiếp tuyến cắt nhau) nên MF cũng là đường cao

=> MF ⊥ AC => $\widehat{AFM}={90}^o$

Xét tứ giác AEMF có

$\widehat{BAC}={90}^o$

$\widehat{AFM}={90}^o$

$\widehat{AEM}={90}^o$

Do đó, AEMF là hình chữ nhật.

b)

Xét tam giác AOM vuông tại A (do AM là tiếp tuyến)

Có:

AE ⊥ MO nên AE là đường cao.

Áp dụng hệ thức lượng trong tam giác ta có:

MA² = ME . MO (3)

Xét tam giác AO’M vuông tại A (do AM là tiếp tuyến)

Có AF ⊥ MO' nên AF là đường cao.

Áp dụng hệ thức lượng trong tam giác ta có:

MA² = MF.MO' (4)

Từ (3) và (4) ME. MO = MF. MO’.

c)

Ta có MA = MB = MC (chứng minh câu a)

Do đó, A, B, C nằm trên đường tròn tâm M bán kính MA, đường tròn này có BC là đường kính do $\widehat{BAC}={90}^o$.

Mặt khác OO' ⊥ MA tại A

Do đó, OO’ là tiếp tuyến của đường tròn tâm M đường kính BC.

d)

Ta có: $\left\{\begin{array}{l}OB\perp BC\\ O\text{'}C\perp BC\end{array}\right.\Rightarrow OB//O\text{'}C$

Do đó, tứ giác OBCO’ là hình thang

Gọi I là trung điểm của OO’.

Ta có M là trung điểm của BC.

Do đó, MI là đường trung bình của hình thang OBCO’

⇒ MI // OB // O'C

Mà $\left\{\begin{array}{l}OB\perp BC\\ O\text{'}C\perp BC\end{array}\right.\Rightarrow MI\perp BC$ (5)

Ta có AEMF là hình chữ nhật nên $\widehat{OMO\text{'}}=\widehat{EMF}={90}^o$

Do đó, tam giác OMO’ vuông tại M

Ta lại có MI là trung tuyến của tam giác OMO’ nên MI = IO = IO’ (tính chất đường trung tuyến ứng với cạnh huyền)

Do đó, O, M, O’ nằm trên đường tròn tâm I đường kính OO’ (6)

Từ (5) và (6) ta suy ra BC là tiếp tuyến của đường tròn tâm I đường kính OO’.