Bài 43 trang 128 - Ôn tập chương II

Lời giải:

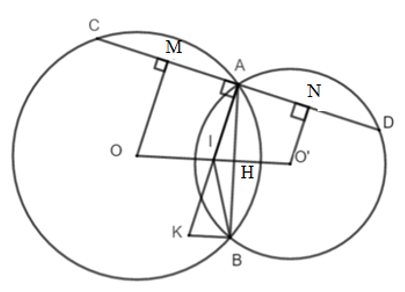
a)

Vẽ OM ⊥ AC tại M, O’N ⊥ AD tại N

Xét đường tròn (O)

Có:

OM ⊥ AC => MA = MC = $\frac{1}{2}$AC (định lý đường kính vuông góc với dây)

Xét đường tròn (O')

Có:

O'N ⊥ AD => NA = ND = $\frac{1}{2}$AD (định lý đường kính vuông góc với dây)

Mặt khác, ta có OM ⊥ CD, IA ⊥ CD, O'N ⊥ CD

=> OM // IA // O'N

Do đó, tứ giác OMNO' là hình thang.

Xét hình thang OMNO'

Có:

IA // OM // O’N

IO = IO’ (I là trung điểm của OO’)

⇒ MA = NA (do đường thẳng song song với hai đáy của hình thang và đi qua trung điểm 1 cạnh bên thì đi qua trung điểm cạnh bên còn lại)

Do đó, 2MA = 2NA ⇒ AC = AD.

b)

Ta có (O) và (O’) cắt nhau tại A, B

Do đó, OO’ là đường trung trực của đoạn thẳng AB (tính chất đường nối tâm của hai đường tròn cắt nhau)

⇒ IA = IB (tính chất đường trung trực của đoạn thẳng)

Mặt khác IA = IK (vì K đối xứng với A qua I)

Do đó, IA = IB = IK = $\frac{AK}{2}$

Xét tam giác KBA

Có BI là đường trung tuyến

BI = $\frac{AK}{2}$

Do đó, tam giác KBA vuông tại B => KB ⊥ AB (đpcm).