Lời giải:

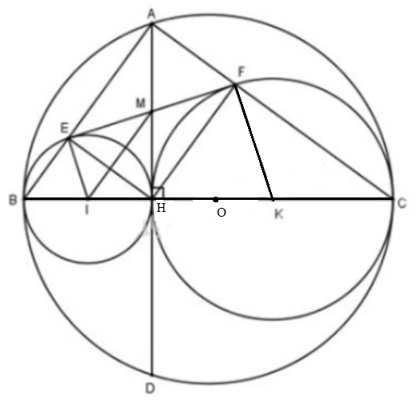
a)

Có :

OI = OB – IB nên (I) tiếp xúc trong với (O)

OK = OC – KC nên (K) tiếp xúc trong với (O)

IK = IH + KH nên (I) tiếp xúc ngoài với (K)

b)

Theo đề bài, ta có:

HE ⊥ AB tại E

=> $\widehat{AEH}={90}^o$

HK ⊥ AC tại F

=> $\widehat{AEH}={90}^o$

Và $\widehat{BAC}={90}^o$ (do A thuộc đường tròn đường kính BC)

Xét tứ giác AEHF có:

$\widehat{EAF}=\widehat{AEH}=\widehat{AFH}={90}^o$

Do đó, tứ giác AEHF là hình chữ nhật.

c)

Xét tam giác ABH vuông tại H có HE là đường cao

Áp dụng hệ thức lượng trong tam giác vuông ta có:

AH² = AE. AB

Xét tam giác ACH vuông tại H có HF là đường cao

Áp dụng hệ thức lượng trong tam giác vuông ta có:

AH² = AF. AC

Do đó, AE. AB = AF. AC (vì cùng bằng AH²)

d)

Gọi M là giao điểm của AH và EF, ta có: ME = MF = MH = MA (do AEHF là hình chữ nhật)

Xét tam giác MEI và tam giác MHI có:

ME = MH

IE = IH (cùng bằng bán kính đường tròn (I))

MI chung

Do đó, tam giác MEI và tam giác MHI bằng nhau (theo trường hợp cạnh – cạnh – cạnh)

=> $\widehat{MEI}=\widehat{MHI}$

Mà AD vuông góc với BC tại H nên $\widehat{MHI}={90}^o\Rightarrow \widehat{MEI}={90}^o$

=> ME ⊥ EI tại E

Mà IE là bán kính đường tròn (I)

Do đó, ME hay EF là tiếp tuyến của đường tròn (I)

Mặt khác ta lại có:

Xét tam giác MFH có:

MF = MH (chứng minh trên)

Do đó, tam giác MFH cân tại M

=> $\widehat{MHF}=\widehat{MFH}$ (hai góc ở đáy) (1)

Xét tam giác KFH có:

KF = KH (cùng bằng bán kính đường tròn (K))

Do đó, tam giác KFH cân tại K

=> $\widehat{KHF}=\widehat{KFH}$ (hai góc ở đáy) (2)

Từ (1) và (2) ta có:

$\widehat{MHF}+\widehat{KHF}=\widehat{MFH}+\widehat{HFK}$ => $\widehat{KFM}=\widehat{MHK}={90}^o$ (do AH ⊥ BC tại H)

=> MF ⊥ FK tại F

Mà KF là bán kính đường tròn (K) nên MF hay EF là tiếp tuyến của đường tròn (K)

Vậy EF là tiếp tuyến chung của hai đường tròn (I) và (K).

e)

EF = AH = $\frac{AD}{2}$.

Do đó EF lớn nhất khi AD lớn nhất. Khi đó, dây AD là đường kính.

Vậy khi dây AD vuông góc với BC tại O thì EF có độ dài lớn nhất.