Bài 36 trang 123

Lời giải:

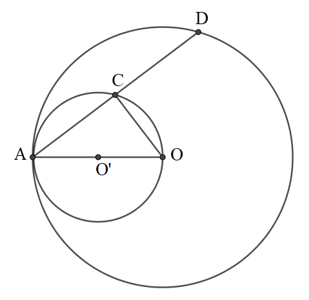
a)

Gọi O’ là tâm của đường tròn đường kính OA

Gọi R và r lần lượt là bán kính đường tròn tâm O và tâm O’.

Độ dài OO’ = d

Vì O’ là tâm của đường tròn đường kính OA nên r = O'A = O'O = $\frac{OA}{2}$

Vì điểm O’ nằm giữa điểm O và A nên ta có:

AO’ + OO’ = OA

⇒ OO’ = OA – O’A hay d = R – r

Do đó, đường tròn (O’) tiếp xúc trong với đường tròn (O).

b)

Xét đường tròn (O’) có A, O, C cùng thuộc đường tròn và cạnh OA là đường kính của đường tròn (O’) nên tam giác CAO vuông tại C

=> OC ⊥ AD tại C

Xét đường tròn (O) có OC là một phần đường kính và AD là dây của đường tròn

Mà OC ⊥ AD tại C (chứng minh trên)

=> CA = CD (do đường kính vuông góc với một dây không đi qua tâm thì đi qua trung điểm dây đó).