Câu 28 Trang 79

Lời giải

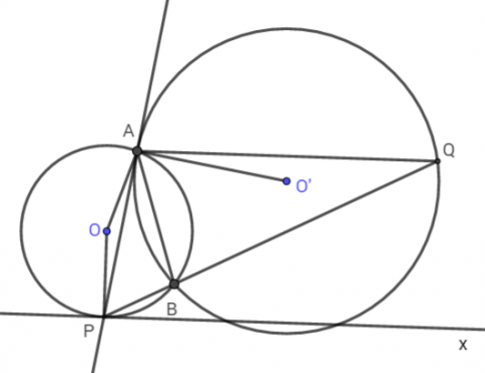
Nối AB.

Ta có:

$\widehat{AQP}$ là góc nội tiếp chắn cung AB của đường tròn (O’) => $\widehat{AQP}$ = $\frac{1}{2}$ sđ cung AB.  (1)

$\widehat{APB}$ là góc nội tiếp chắn cung AB của đường tròn (O) => $\widehat{APB}$ = $\frac{1}{2}$ sđ cung AB.  (2)

Từ (1) (2) suy ra: $\widehat{AQP}$ = $\widehat{APB}$   (4)

Lại có: $\widehat{APB}$ là góc nội tiếp chắn cung AB của đường tròn (O)

            $\widehat{BPx}$ là góc tạo bởi tia tiếp tuyến Px và dây cung PB của đường tròn (O) 

=> $\widehat{APB}$ = $\widehat{BPx}$ (hệ quả)     (4)

Từ (3), (4) suy ra: $\widehat{AQP}$ = $\widehat{BPx}$ mà hai góc ở vị trí so le trong nên AQ // Px.