Bài 1: Một số hệ thức về cạnh và đường cao trong tam giác vuông

I. Khái niệm

Cho tam giác ABC vuông tại A , ta có :

• Cạnh huyền : BC
• Cạnh góc vuông : AB , AC
• Đường cao : AH
• Hình chiếu :

• • BH là hình chiếu của AB lên BC .
  • CH là hình chiếu của AC lên BC .

1. Hệ thức giữa cạnh góc vuông và hình chiếu của nó trên cạnh huyền

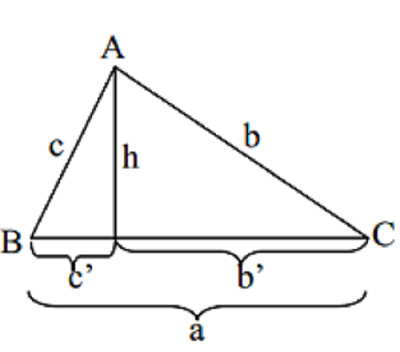
Định lí 1 

Trong một tam giác vuông, bình phương mỗi cạnh góc vuông bằng tích của cạnh huyền và hình chiếu của cạnh góc vuông đó trên cạnh huyền

• $AB^{2}=BC.BH$
• $AC^{2}=BC.CH$

=> Định lí Py-ta-go :  $BC^{2}=AB^{2}+AC^{2}$

2. Một số hệ thức liên quan tới đường cao

Định lí 2

Trong một tam giác vuông, bình phương mỗi cạnh góc vuông bằng tích của cạnh huyền và hình chiếu của cạnh góc vuông đó trên cạnh huyền

• $AH^{2}=BH.CH$

Định lí 3

Trong một tam giác vuông, bình phương mỗi cạnh góc vuông bằng tích của cạnh huyền và hình chiếu của cạnh góc vuông đó trên cạnh huyền

• $AB.AC=BC.AH$

Định lí 4

Trong một tam giác vuông, bình phương mỗi cạnh góc vuông bằng tích của cạnh huyền và hình chiếu của cạnh góc vuông đó trên cạnh huyền

• $\frac{1}{AH^{2}}=\frac{1}{AB^{2}}+\frac{1}{AC^{2}}$