Bài 39 trang 123 - Vị trí tương đối của hai đường tròn

Lời giải:

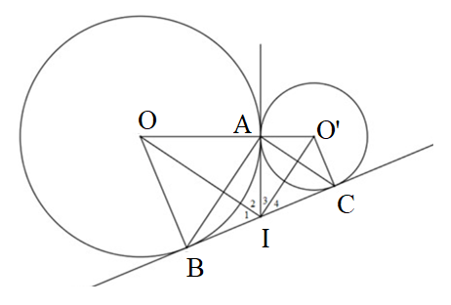
a)

Xét đường tròn (O) có IB, IA là hai tiếp tuyến lần lượt tại B, A; IB và IA giao nhau tại I.

⇒ IB = IA (tính chất hai tiếp tuyến cắt nhau) (1)

Xét đường tròn (O’) có IC, IA là hai tiếp tuyến lượt tại C, A; IC và IA giao nhau tại I.

⇒ IC = IA (tính chất hai tiếp tuyến cắt nhau) (2)

Từ (1) và (2) ta có: IB = IC = IA = $\frac{1}{2}$BC

Xét tam giác ABC có

I là trung điểm của BC (do IB = IC)

Do đó, AI là trung tuyến ứng với cạnh BC

Mà IA = $\frac{1}{2}$BC (chứng minh trên)

Do đó, tam giác ABC vuông tại A (do tam giác có đường trung tuyến ứng với một cạnh bằng nửa cạnh đó thì tam giác đó là tam giác vuông)

=> $\widehat{BAC}={90}^o$.

b)

Xét đường tròn (O) có IB, IA là hai tiếp tuyến lần lượt tại B, A; IB và IA giao nhau tại I.

Do đó, IO là tia phân giác của góc BIA => $\widehat{I_1}=\widehat{I_2}$

Xét đường tròn (O’) có IC, IA là hai tiếp tuyến lượt tại C, A; IC và IA giao nhau tại I.

Do đó, IO’ là tia phân giác của góc CIA => $\widehat{I_3}=\widehat{I_4}$

Lại có $\widehat{I_1}+\widehat{I_2}+\widehat{I_3}+\widehat{I_4}={180}^o$

=> $2\widehat{I_2}+2\widehat{I_3}={180}^o$ (do $\widehat{I_1}=\widehat{I_2}$, $\widehat{I_3}=\widehat{I_4}$)

=> $\widehat{I_2}+\widehat{I_3}={90}^o$

=> $\widehat{OIO\text{'}}={90}^o$.

c)

Vì IA là tiếp tuyến chung của hai đường tròn nên IA ⊥ OA, IA ⊥ O'A

=> IA ⊥ OO' tại A

Xét tam giác OIO’ vuông tại I

Có IA là đường cao (do IA ⊥ OO')

Áp dụng hệ thức lượng trong tam giác vuông ta có:

AI² = AO.AO' = 9.4 = 36

=> AI = $\sqrt{36}$ = 6 (cm)

Có BC = 2AI (chứng minh phần a)

⇒ BC = 2.6 = 12 (cm).